Gesture Recognition and Recurrent Neural Networks on an Arduino

Brief review: Neural Networks and Recurrent Neural Networks

As you can see in the detailed resources cited above, an artificial neuron is a small piece of code that:

• takes numerical input values (one value per “synapse”)
• sums them up with by giving each one varying degree of importance in the sum (its “weight” or the strength of the synapse)
• applies a “threshold function”, i.e. it responds differently if the sum is small or large
• outputs this final value

Thus, by layering such artificial neurons we can input the motion sensor data and output, after a few layers, a number representing the gesture we have been performing while holding the device. A very important step would be to teach or “train” the neural network how to make that decision. Just like in biology, this will be done by changing the strength of the connections between the neurons, i.e. by finding appropriate values for the aforementioned weights.

By grouping the neurons in layers it becomes easier to write down the necessary computer code as standard linear algebra operations. Moreover, as gesture recognition requires understanding the entire history of a motion, we will dedicate a few neurons to work as a memory, turning our neural network into a recurrent neural network. This leads us to our architecture of choice.

The Recurrent Neural Network of choice for our task

Our motion sensor can easily report measured acceleration and rotation 50 times a second. This will be the input for our recurrent neural network: a 6-dimensional vector containing the acceleration \(\vec{a}\) and rotation speed \(\vec{\omega}\) components for each of the 3 directions of space: \[\text{input vector:}\ \ \ \vec{v}_\textrm{in} = (a_x,a_y,a_z,\omega_x,\omega_y,\omega_z).\] We will also reserve a vector \(\vec{s}\) as a memory. With each new measurement sent to the network (50 times a second), we will update that memory in the following way: \[\text{memory update rule:}\ \ \ \vec{s}\leftarrow \sigma(W_s\cdot\vec{s}+U\cdot\vec{v}_\textrm{in}+\vec{b}_s),\] Where the matrices \(W_s\) and \(U\) (synapse connection weights) as well as the vector \(\vec{b}_s\) (bias) are parameters to be trained. \(\sigma\) is the thresholding function, for which we have chosen to use \(\textrm{relu}\), because it is easy to compute on simple hardware.

Out of this memory we can now compute the output of the recurrent layer of the neural network: \[\text{recurrent layer output:}\ \ \ \vec{v}_\textrm{rec}=\sigma(W_o\cdot\vec{s}+\vec{b}_o),\] where \(W_o\) and \(\vec{b}_o\) are more parameters that need to be trained.

We can repeat multiple such recurrent layers, where the output of the previous layer is used as an input for the next layer with its own unique memory vector. We ended up using 2 recurrent layers for our implementation, but a typical 16MHz arduino can run quite a few more of them at a rate of 50Hz if necessary. Our memory vectors and our output vectors all have 6 dimensions.

At the very end of the neural network, we need to take the output of the last recurrent layer and turn it into a decision of which gesture is being performed. For simplicity we will use only three rather simple gestures for our first network:

• keeping the device steady
• shaking the device in one direction
• shaking the device in the orthogonal direction

Thus, our output vector \(\vec{v}_\textrm{out}\) will have three components, each representing the probability (or certainty of belief) that the device is performing the corresponding gesture. As they need to sum up to one, it is natural to use the \(\textrm{softmax}\) function on a final non-recurrent neural network layer: \[\text{classification result:}\ \ \ \vec{v}_\textrm{out}=\textrm{softmax}(W\cdot\vec{v}_\textrm{rec}+\vec{b}),\] where \(W\) and \(\vec{b}\) are the final set of parameters in need of training.

Implementing a Recurrent Neural Network on an Arduino

The typical Arduino hardware does not directly support floating point numbers. The compiler still lets you use them, but the generated machine code emulates them by using the underlying integer data types. This emulation is usually judged to be much too slow, as a simple multiplication of two floating point numbers will take much longer than the time for an integer numbers multiplication. If this significant overhead is making our network too slow for the 50Hz rate at which we want to run it, we can retrain the network to use only integers. This is, however, much more succeptible to bugs, so let us first benchmark the performance of a typical floating point network running on a 16MHz Arduino.

We will need to implement a mock neural network to do these tests. This net.h file (also embedded below) contains such an implementation, together with all the linear algebra operations that we will need.

The network() function at the bottom of that file is the one that looks at the globally defined array input, computes one iteration of our recurrent neural network on it, and stores the results in the globally defined array output. It then finds which element of output is the largest, and reports it as the most probable gesture being recorded by the device.

The entirety of the user code, assuming net.h contains properly trained parameters, would then be

SpinWheel.readIMU(); // read the motion sensor
input[0] = SpinWheel.ax; // acceleration components
input[1] = SpinWheel.ay;
input[2] = SpinWheel.az;
input[3] = SpinWheel.gx; // rotation speed components
input[4] = SpinWheel.gy;
input[5] = SpinWheel.gz;
c = network(); // accesses `input` as a global variable

where most of the lines simply move measurement data from the sensor to the neural network code. At the end the variable c contains the number representing the most probable gesture according to the neural network. At that point c can be used as a trigger to perform other operations on the device, e.g. lighting up the LEDs in a pretty pattern to acknowledge the detected gesture.

By using the millis() function (which reports number of milliseconds since the device has started) we can measure how slow the neural network computation is. The entirety of the code described above takes 7.2ms (7.2 thousands of a second), out of which 2.3ms are dedicated to communicating with the motion sensor. This leaves plenty of space in our 20ms (i.e. 50Hz) time budget for many more additional layers in our neural network or for using more advanced types of memory (like an LSTM or GRU recurrent networks). We will explore these topics later on, as a way to enable more advanced types of gesture recognition.

Regulating the pace of the computation

Now that we know we are fast enough, we need to ensure that each measurement and each neural network computation are done at regular intervals. Otherwise a small change in our neural network architecture might significantly change the rate at which we are acquiring measurements, because of the computation taking longer. Instead, we will simply ensure that each computation starts at regular intervals and takes less time than the length of the interval, without worrying exactly how long that is. We can do this by defining a pacer function:

void pacer(long period_ms) {
  static long t = millis(); // a variable preserved between function runs
  while(millis()-t < period_ms){} // constantly checking the time
  t += period_ms; // recording the last time `pacer` finished
}

Can you see how this function is different from simply using delay()?

Now the entirety of our user code is:

void loop() {
  pacer(20); // run only on 20ms intervals
  SpinWheel.readIMU(); // read the motion sensor
  input[0] = SpinWheel.ax; // acceleration components
  input[1] = SpinWheel.ay;
  input[2] = SpinWheel.az;
  input[3] = SpinWheel.gx; // rotation speed components
  input[4] = SpinWheel.gy;
  input[5] = SpinWheel.gz;
  c = network(); // accesses `input` as a global variable
  // do something based on the value of `c`
}

Implementing the same neural network in Python

We will need to train the neural network, and regrettably the microcontroller of the SpinWheel can be too slow for that. Instead, we will gather the necessary data from the SpinWheel, but run the training procedure on a separate computer. It is straightforward to reimplement our neural network in numpy or tensorflow, two popular Python libraries for numerical computation (tensorflow in particular provides us with the gradients for free). Other popular options are jax and pytorch, but in all of these libraries the code would look virtually the same.

We start by implementing a generic single layer RNN, implementing the previously mentioned math in code:

def rnn_step(state, v_in, Ws, U, Bs, Wo, Bo):
    new_state = relu(Ws@state + U@v_in + Bs)
    v_out = relu(Wo@new_state+Bo)
    return new_state, v_out

Here @ denotes matrix multiplication.

The neural network as a whole will repeatedly apply two such RNN layers to the incoming measurements in order to get us the output vector of probabilities. To set the notation, we will denote the parameters of the network as W1s, U1, W1o, B1s, B1o, W2s, U2, W2o, B2s, B2o, Wout, Bout: these are the same matrices and bias vectors discussed earlier. The final neural network would look like:

def model_step(state1, state2, v_in):
    # RNN layer 1
    state1, v1 = rnn_step(state1, v_in, W1s, U1, B1s, W1o, B1o)
    # RNN layer 2
    state2, v2 = rnn_step(state2, v1  , W2s, U2, B2s, W2o, B2o)
    # Last NN layer (no memory, softmax activation)
    v_out = Wout@v2 + Bout
    v_out = exp(v_out)
    v_out /= sum(v_out) # The final probability vector
    return state1, state2, v1, v2, v_out

Applying our 2D array of measurements is now a simple python loop as seen below. The recorded_input object is an N-by-6 array, where N is the number of recordings taken from the motion sensor (and 6 for the other dimension, because of the 3 acceleration + 3 rotation measurements taken each time).

output = [] # To contain all output results.
state1 = np.zeros(6) # Initially the memories
state2 = np.zeros(6) # are all set to zero.

for row in recorded_input:
    state1, state2, v1, v2, v_out = model_step(state1, state2, row)
    output.append(v_out)

Using the scan function for higher performance

Python loops can be rather slow. Different numerical libraries address this problem differently, but tensorflow in particular lets you use a function called scan to run through an entire array and apply a given routine efficiently to each element. Importantly, it also lets you save accumulated values. As such, it is a general version of the map and reduce functions from many other languages.

To use it, we will first restructure our input recordings. That would make the training of the network easier as well. Instead of N recordings, each of 6 values, we will cut up all these N recordings into multiple shorter fixed-duration recordings. For instance, we cut all records into sequences of 50 samples, leaving us with roughly \(N/50\) such records. We can stack them, resulting in a three-axis array with dimensions 50-by-6-by-n where \(n\approx N/50\).

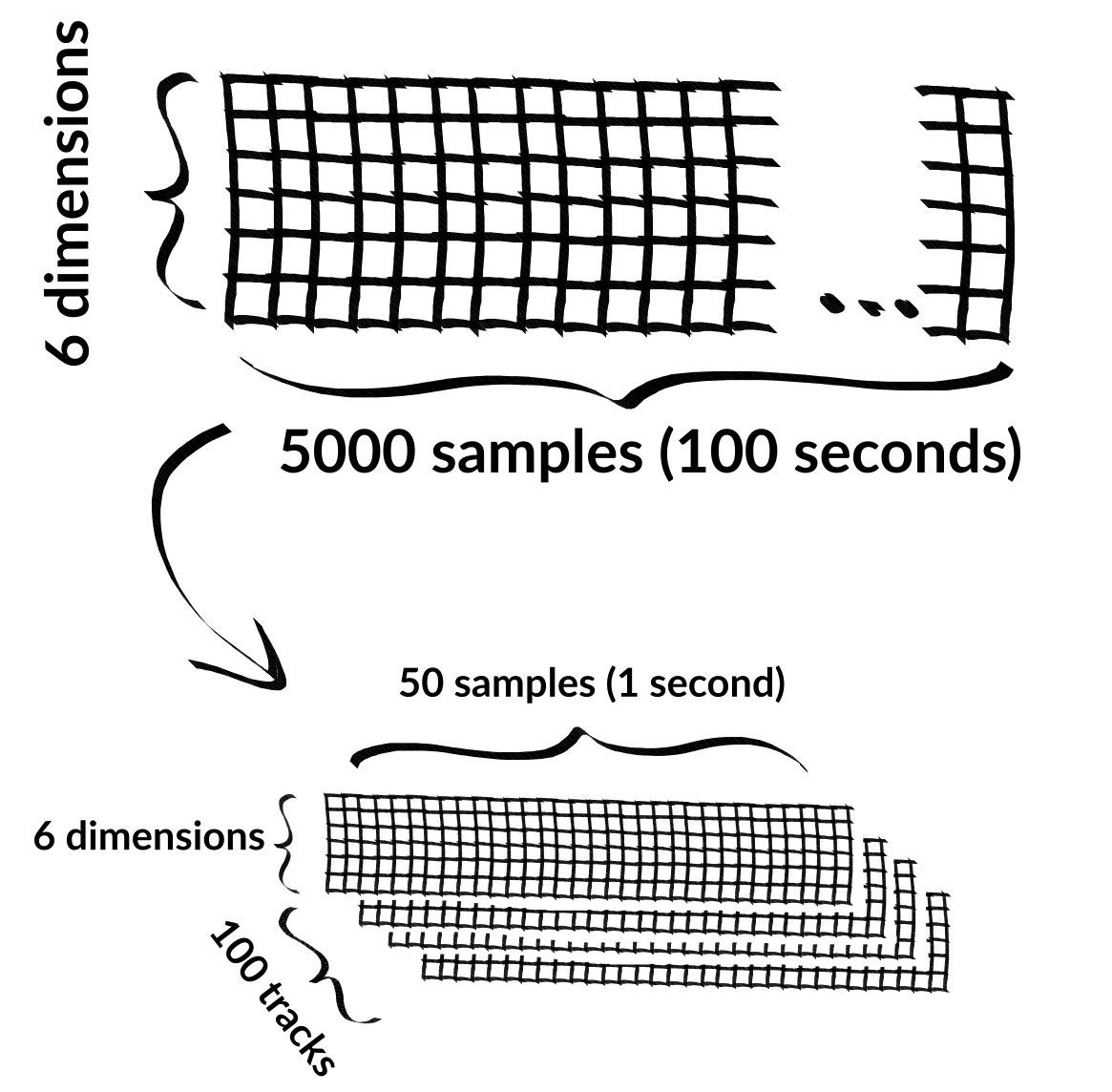
Now we can simply apply our first RNN layer to the entirety of the recorded data (which we will denote simply x to keep with conventions).

states, v1_outs = tf.scan(
    lambda state_vout, v_in: rnn_step(state_vout[0], v_in, W1s, U1, B1s, W1o, B1o),
    x,
)

Now v1_outs is a vector with the same dimensions as x, but instead of containing the input recordings at a given time step, it contains the outputs of the first RNN layer at that same time step.

The entire model becomes:

def model(x,
          W1s, U1, W1o, B1s, B1o,
          W2s, U2, W2o, B2s, B2o,
          Wout, Bout,
          initializer=tf.random.normal):
    # first RNN layer
    _, v1_outs = tf.scan(
        lambda state_vout, v_in: rnn_step(state_vout[0], v_in, W1s, U1, B1s, W1o, B1o),
        x,
        initializer = (initializer((neurons_1s,x.shape[2])), x[0,...])
    )
    # second RNN layer
    _, v2_outs = tf.scan(
        lambda state_vout, v_in: rnn_step(state_vout[0], v_in, W2s, U2, B2s, W2o, B2o),
        v1_outs,
        initializer = (initializer((neurons_2s,x.shape[2])), x[0,...])
    )
    # Last NN layer (no memory, softmax activation)
    y_model = tf.einsum('ij,TjS->TSi', Wout, v2_outs) + Bout
    y_model = tf.nn.softmax(y_model, axis=2)
    return y_model

Notice the initializer term in this function. This decides whether the initial values for state1 and state2 (the memories of the two RNN layers) should be simply zeroes or should be random values. If we want the network to work robustly, the initial value of the memory should not matter much, and we will need to ensure this is indeed the case during training. One way to do that is to train with random initial values for the memory as enabled by the code above.

Training the neural network

Now that we finally have the network implemented both on the microcontroller and on our computer, we can go ahead and train it. To do that, we need to gather the motion sensor data from the SpinWheel, while performing the gestures we want to learn. We can do that by simply adding some printing code to our SpinWheel code and recording the transmitted data through a USB cable to our computer. An example logging code could look like this:

for (i=0; i<6; i++) {
  Serial.print(input[i]);
  Serial.print(' ');
}
Serial.println();

And for the training, we just need to reformat this recording into a sequence of smaller recordings as discussed above and run a gradient descent through tensorflow:

with tf.GradientTape() as tape:
    # calculating the model prediction
    y_model = model(x,
                    W1s, U1, W1o, B1s, B1o,
                    W2s, U2, W2o, B2s, B2o,
                    Wout, Bout,
                    #initializer=tf.zeros,
                   )
    # picking only the last few results from the record
    y_model = y_model[burnin:,:,:]
    # calculating the error between the model and the training data
    err = tf.reduce_mean((y_model-y_onehot)**2)
    # adding a regularization term
    reg = tf.reduce_mean([tf.reduce_mean(tf.abs(_)) for _ in variables])
    total_loss = err+0.05*reg
# calculating the gradient
grads = tape.gradient(total_loss, variables)
opt.apply_gradients(zip(grads, variables))

By repeating this step a few hundred times we can train the network to indeed predict what gesture we are performing based on the motion data. There are a couple of things to note here:

• The training procedure would have easier time finding good parameters if we first start with zeroed-out initial memory values (i.e. initializer=tf.zeros);
• However, this would be unrealistic for the real-life performance of the network. Therefore, after some initial training with zeroed-out memory, we should continue the training runs by setting the initial values of the memory to random numbers. This would ensure the network works well independently of the length of recordings we are giving to it.

The effect of such a switch, from zero to random initializer, can be observed in the history of our training runs:

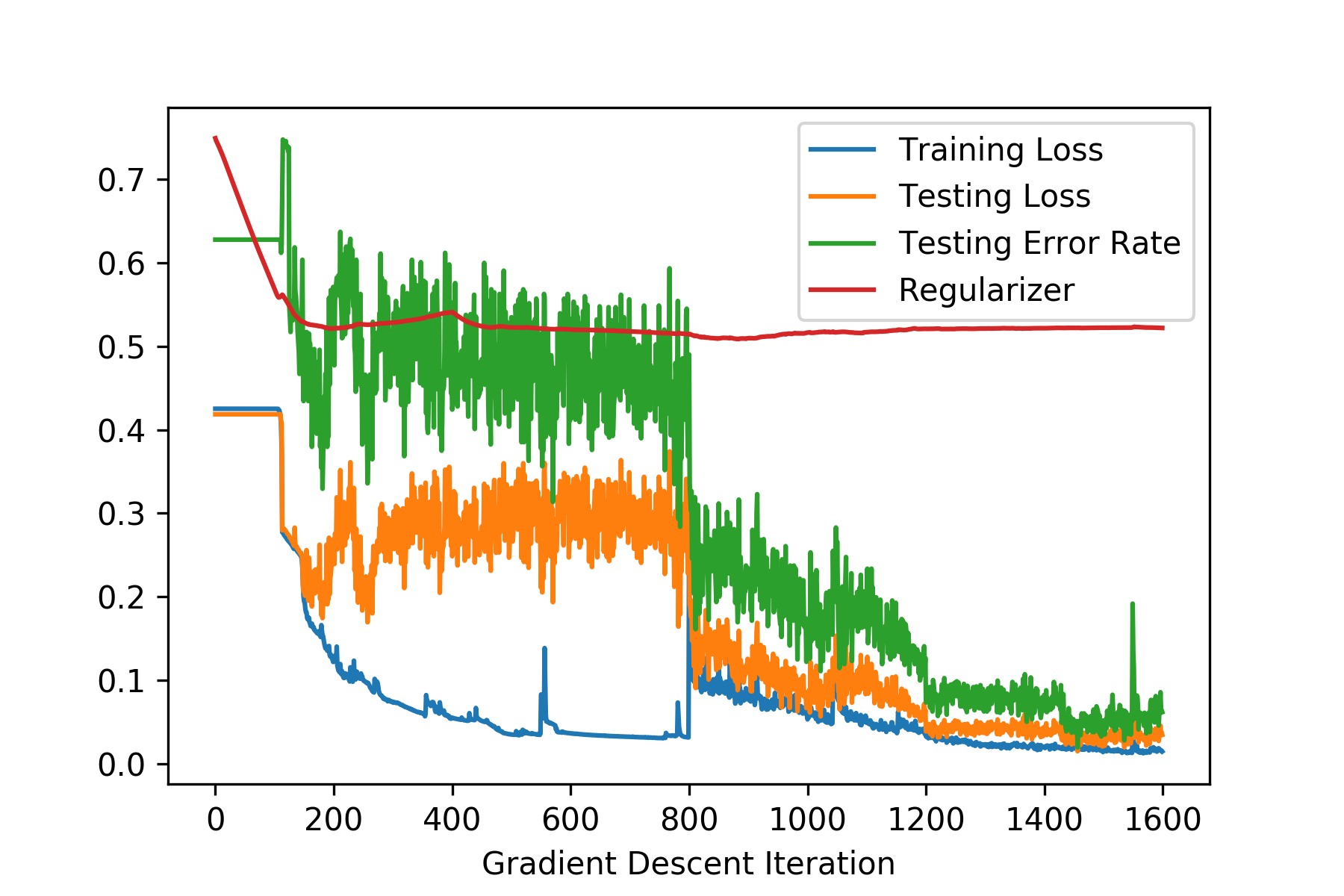
• We did not use the entire recording in our cost function. Instead of basing our error estimate on y_model we used only a fraction of the data in that array, namely y_model[burnin:,:,:]. I.e. we skipped the first burnin number of predictions. This is in order to give the network enough time to settle on a decision after seeing new measurement data. One can play with that value in order to get faster decisions, maybe even anneal it. Another option is to utilize a smoother weighting of each data point instead of an abrupt cutoff.

Visualizing the results and the information flow through the network itself

It would be a significant understatement to say that understanding how a neural network decides what prediction to give is difficult. Especially in the case of deep neural networks with layers upon layers of neurons, it is still an open area of research to interpret their behavior. We can perform a humble attempt of our own to do that same task. Thankfully our network is rather small, so it is feasible to represent it graphically:

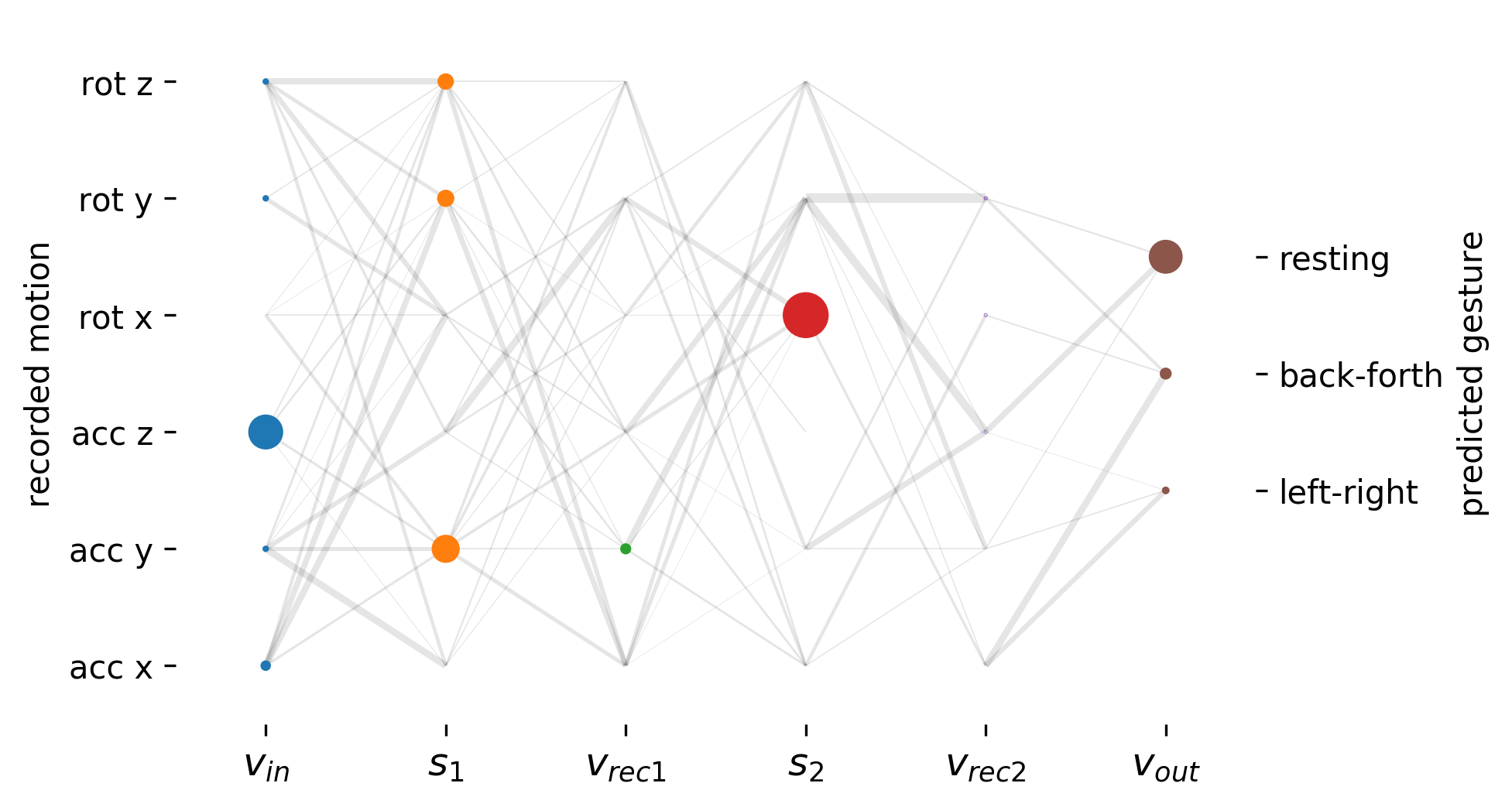
On its own, such a visualization does not immediately give too much useful information. But we can create an animation of the entire history of the network, which might be more elucidating. We will also pair it up with an actual recording of the device (you might want to full-screen it):

A few question spring here:

• Some neurons become very active, but their outgoing connections are weak (thin lines). Is this desired or is the network unnecessary convoluted?
• Many neurons in the same layer seem to respond in the same way. Does this mean we do not need such larger layers?
• Even neurons deep in the network seem to respond mostly to the immediate motion measurement, not to the overall gesture. Is this is a desired feature or is it a sign of a bad architectural decision?

Some of these question go against the standard approach of deep learning, where we just explode the number of training parameters, hopefully making the cost landscape easier to train on. However, such questions of simplifying our neural network might be important when we want to run them on simple underpowered hardware.

Next Steps

There are a number of important steps to take in order to understand this setup better and improve upon it. The next guide would explore:

• Was it really necessary to use a neural network for this task? Look at the video above and how noticeable the x and y accelerations were. Maybe we can simply use a low-pass filter that takes the magnitudes of the x and y accelerations and makes the decisions purely based on that. This would certainly work for the simple gestures we picked here, but it will not work well for a general gesture. Moreover, this type of “feature engineering” (the technical term for cherry-picking parts of the signal manually) needs to be redone for every new gesture. On the other hand, a neural network simply needs to be trained on the new training data without much extra thought being put into it.
• Can we force our network, through judicious use of regularization, to learn a simpler model, like the one above, on its own. After all, this is the whole reason for regularization: to steer the learning process away from unnecessarily convoluted and overfitting models. Until recently this was a very popular notion in machine learning: that we should look at the simplest and smallest neural net. While in the present case we can probably do it, this approach does not scale. It turns out that it is much easier to train significantly overparameterized system than to train a small neural net. This is the big surprise the recent progress in deep neural networks taught us: while the extra parameters are “unnecessary”, they make the learning process drastically easier.
• We know that LSTM and GRU architectures can run on the SpinWheel and other Arduino-compatible hardware (both in terms of clock-rate and RAM). Such architectures are much better at “remembering” the recent past and will be indispensable for advanced gesture recognition. This will be the main next step in this series of educational activities.
• If we switch to using only integers the network can be an order of magnitude larger.
• The output of the network can be a bit jittery (observe the last layer from the video above). A low-pass filter on that output might be a useful postprocessing addition to the model.

And here you can find the python code used for training and visualization of the network.